金融数学 学了啥(下) —— 金融模型
微信公众号内容地址: https://mp.weixin.qq.com/s/reIL0yqa0bw1VF0onYwOGA
简单来说,金融数学的目标就是用数学模型给金融产品定价,例如从未来的价值($T$ 时刻),倒推现价($t$ 时刻或 $0$ 时刻)。
就课程来说,核心是两大部分,即金融产品和金融模型;同时金融模型体系中也包含一定的数学基础。
- 金融产品: 存款&利率,债券,常见的金融衍生品——远期合约、期货、期权
- 数学基础: 微分和积分,概率论——期望、方差和正态分布
- 金融模型: 伯努利模型,B-S 模型(Black-Scholes,布莱克-舒尔斯公式)
作为下篇,我们将主要集中在金融模型部分(因而不可避免要涉及一些数学基础)。
数学基础
常用的微分/偏微分
主要应用在
-
伊藤引理中,需要求一阶和二阶偏导 $\frac{\partial f}{\partial x},\frac{\partial^2 f}{\partial x^2},\frac{\partial f}{\partial t} $
\[\begin{aligned} d(e^x)=e^xdx \end{aligned}\] \[d(x^\mu)=\mu x^{\mu-1}dx\]
常用的积分/定积分
主要应用在
- 伊藤引理使用后,通过 $dY_t$ 得到 $Y_t$,完成求解微分方程
- 布朗运动及 B-S 模型下,连续型随机变量的数学期望 $E(X)$,方差 $Var(X)$ 的计算
分部积分
\[\int f(x)g'(x)dx = f(x)g(x) - \int f'(x)g(x)\]正态分布相关
\[\begin{aligned} \int_{-\infty}^{+\infty} e^{-\alpha x^2}dx = \sqrt{\frac{\pi}{\alpha}},\\ (\int_{-\infty}^{+\infty} e^{-\frac{x^2}{2}}dx = \sqrt{2\pi}) \end{aligned}\]Gamma 函数
\[\begin{aligned} \Gamma(z)&=\int_{0}^{+\infty} t^{z-1}e^{-t}dt \\ &= (z-1)\Gamma(z-1),\\ &(\Gamma(1)=1,\Gamma(\frac{1}{2})=\sqrt{\pi}) \end{aligned}\]概率论,连续型随机变量
主要应用在
- 布朗运动的判断(符合正态分布,且不同时刻相互独立)
- 计算伊藤过程的数学期望和方差
概率密度函数 $f(x)$
\[\int_{X}f(x)dx=1\] \[P(a \le X \le b) = \int_{a}^{b}f(x)dx\]数学期望 $E(X)$
\[\begin{aligned} E(X)=\int_{-\infty}^{+\infty}xf(x)dx,\\ E(g(X))=\int_{-\infty}^{+\infty}g(x)f(x)dx \end{aligned}\] \[E(C)=C,C是常数\] \[E(aX)=aE(X),a是常数\] \[\begin{aligned} E(aX+bY+c)=aE(X)+bE(Y)+c,\\ a和b是常数 \end{aligned}\] \[\begin{aligned} 若X,Y &相互独立,\\ &则E(XY)=E(X)E(Y) \end{aligned}\]方差 $Var(X)$
\[\begin{aligned} Var(X)&=E((X-\mu)^2)\\ &=E(X^2)-(E(X))^2 \end{aligned}\] \[Var(C)=0,C是常数\] \[Var(aX)=a^2Var(X), a是常数\] \[\begin{aligned} Var(&aX+bY+c)\\ &=a^2Var(X)+b^2Var(Y),\\ &a、b、c是常数 \end{aligned}\]协方差 $Cov(X,Y)$
\[\begin{aligned} Cov(X,Y)&=E[(X-E(X))(Y-E(Y))]\\ &=E(XY)-E(X)E(Y) \end{aligned}\] \[\begin{aligned} Cov(X,Y)&=0,\\ &即E(XY)=E(X)E(Y),\\ &则X,Y相互独立 \end{aligned}\]一维正态分布 $N(\mu, \sigma^2)$
\[概率密度函数 f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\] \[E(X)=\mu,Var(X)=\sigma^2\] \[标准正态分布 N(0,1),f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\]标准正态分布累积分布函数 CDF $N(d)$
\[N(d)=P(X \le d) = \int_{-\infty}^{d}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\]指示函数 $\mathbb{1}_A$
\[\mathbb{1}_{S_T > K} = \begin{cases} 1 & \text{if } S_T > K \\ 0 & \text{otherwise} \end{cases}\]金融模型
对于金融模型,主要关注市场假设,即股票 $S$ 如何进行变化;以及在这样的市场假设下,如何进行金融产品的定价。
对于伯努利模型:
- 其市场假设就是每个时间序列内,股票价格一定概率上升到一个值,一定概率下降到另一个值;因而股票的变化其实可以近似以二叉树的形式表现。
- 对衍生品 $X$ 的定价策略,在每一序列通过等价投资组合 $h(x,y)$ + 单一价格定律来计算;
- 进一步的,通过数学推导,该衍生品 $X$ 的定价可以用"风险中立概率"下的该衍生品的平均价格进行贴现。
- 整体过程类似: 计算 $t=n$ 的平均价格,贴现得到 $t=n-1$ 上各节点的价格;再贴现得到 $t=n-2$ 上各节点的价格…
对于 B-S 模型:
- 其市场假设相比于伯努利模型,由离散型转向连续型
- 一方面在每个时间序列内来看,增加了随机波动,股票价格不仅仅是上升或下降到一个固定的值,而是有个随机波动的区间和概率,自然联想到正态分布可以满足。
- 另一方面,时间也从离散的时间序列,扩展到连续的时间区间 $[0,T]$。
- 综合以上,布朗运动的概念可以满足这两方面。在每一个时刻 $t \in [0,T] $,随机波动 $W_t$ 服从 $N(0,t)$ 的正态分布(即随着时间推移,股票波动的上下限越来越大)
- 基于此,在 B-S 模型中,市场假设为指数布朗运动
- 衍生品的定价,来自于让其价格变动和股票价格变动的差值与利率 $r$ 相关,即希望 $dI(t) = df(t, St) - △dSt = rI(t)dt$
- 该随机微分方程($SDE$,包含了随机变量项),需要新的数学求解法,因而需要借助伊藤引理。
- 求解之后,会得到一个偏微分方程,即为B-S 偏微分方程($PDE$),求解需要借助费曼-卡茨公式(Feynman–Kac formula),转换为随机过程的条件期望(实际上,这就是”风险中立下,衍生品的平均价格”对应到连续型变量的形式)。
-
求解该条件数学期望
后,最终可以得到目标衍生品的定价。
伯努利模型
伯努利模型——单一时间序列
市场假设 $S$
- $0 < d<1<\mu$,离散时间序列 $t$ 从 $0$ 变化到 $1$
- 一只股票 $S_0$,有 $p_\mu$ 的概率 $S_1=\mu S_0$;有 $p_d$ 的概率 $S_1=dS_0$

套利条件
- 该市场为无套利市场,当且仅当 $d<1+r<\mu$
风险中立概率 $Q$ 和期望
- 即不考虑真实的 $p_\mu$ 和 $p_d$,在 $q_\mu$ 和 $q_d$ 下,股票的预期收益持平利率 $1+r$
衍生品 $X$,等价投资组合 $h(x,y)$ 和 风险中立定价
- $X = \Phi(\mu)$,表示股票上升到 $\mu S_0$ 时,衍生品的回报
- $h(x,y)$,表示投资组合,持有 $x$ 份存款,和 $y$ 份股票 $S$ ($x,y$ 可以为负)
- 若 $X$ 和 $h(x,y)$ 在 $t=1$ 时价格相等,则他们在 $t=0$ 时价格也相等。
- $t=1$, \(\left\{ \begin{aligned} &\Phi(\mu) = x(1+r) + y\mu S_0\\ &\Phi(d) = x(1+r) + yd S_0\\ \end{aligned} \right. => \left\{ \begin{aligned} &x = \frac{1}{1+r} \frac{\mu \Phi(d) - d\Phi(\mu)}{\mu-d}\\ &y = \frac{1}{S_0} \frac{\Phi(\mu) - \Phi(d)}{\mu -d}\\ \end{aligned} \right.\)
- $t=0$, \(\begin{aligned} \Pi_0(X) &= V_0^h \\ &= x + yS_0 \\ &= ... \\ &= \frac{1}{1+r}(\Phi(\mu)q_\mu + \Phi(d)q_d)\\ &= \frac{1}{1+r}E^Q(X) \end{aligned}\)
- 数学推导可知,实际上 $X$ 的定价可以由"风险中立概率"下的数学期望价格 + 贴现得到。
例 $1$: 年度连续型复利 $r=5\%$,考虑伯努利模型,一只股票 $S_0=40$,一年后各有 $50\%$ 概率为 $45$ 和 $39$;计算欧式看跌期权的定价(到期日为 $1$ 年,行权价格为 $41$)
1、 伯努利树
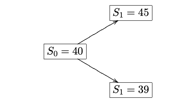
2、 风险中立概率
\[\mu = 45/40 = 1.125,d=39/40=0.975\] \[\left\{ \begin{aligned} &q_\mu + q_d = 1\\ &q_\mu*\mu + q_d*d = e^r\\ \end{aligned} \right. => \left\{ \begin{aligned} &q_\mu = 0.508\\ &q_d = 0.492\\ \end{aligned} \right.\]3、 $t=1$ 时,$\Phi(X)=(41-S_1)^+$
4、 定价为:
\[\begin{aligned} \Pi_0(X) &= e^{-0.05}(q_\mu (41-45)^+ + q_d (41-39)^+)\\ &=e^{-0.05}(0 + 0.492*2) \\ &=0.936 \end{aligned}\]伯努利模型——多时间序列
市场假设 $S$
- $0 < d<1<\mu$,离散时间序列 $t$ 从 $0$ 变化到 $n$
- 从 $t=i$ 到 $t=i+1$,一只股票 $S_i$,有 $p_\mu$ 的概率 $S_{i+1}=\mu S_i$;有 $p_d$ 的概率 $S_{i+1}=dS_i$

定价
与单一时间序列相似,从 $t=i+1$,由"风险中立概率"下的数学期望价格 + 贴现得到 $t=i$ 时刻的价格;并一直计算到 $t=0$。
例 $2$: 年度连续型复利 $r=4\%$,考虑伯努利模型,一只股票 $S_0=40$,每一个序列(三个月)内,要么上涨或下跌 $10\%$,一直进行三个序列;计算欧式看涨期权的定价(到期日为 $9$ 个月,行权价格为 $45$)
1、 伯努利树
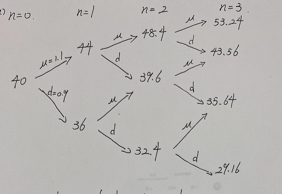
2、 风险中立概率(每个序列-$3$ 个月,均相同)
\[\mu = 1.1,d=0.9,r=0.04/4=1\] \[\left\{ \begin{aligned} &q_\mu + q_d = 1\\ &q_\mu*\mu + q_d*d = e^r\\ \end{aligned} \right. => \left\{ \begin{aligned} &q_\mu = 0.5503\\ &q_d = 0.4497\\ \end{aligned} \right.\]3、 $t=3$ 时,$\Phi(X)=(S_3-45)^+$
4、 定价为:
\[\begin{aligned} t=3,\\ &\Pi_3(X)|_{S_3(\mu \mu \mu)}=8.24\\ &\Pi_3(X)|_{S_3(\mu \mu d)}=0\\ &\Pi_3(X)|_{S_3(\mu d d)}=0\\ &\Pi_3(X)|_{S_3(d d d)}=0\\ t=2,\\ \Pi_2(X)|_{S_2(\mu \mu )} &= e^{-r}(q_{\mu}\Pi_3(X)|_{S_3(\mu \mu \mu)}+q_d\Pi_3(X)|_{S_3(\mu \mu d)})\\ &=4.4894\\ \Pi_2(X)|_{S_2(\mu d )} &= e^{-r}(q_{\mu}\Pi_3(X)|_{S_3(\mu d \mu)}+q_d\Pi_3(X)|_{S_3(\mu d d)})\\ &=0\\ \Pi_2(X)|_{S_2(d d )} &= e^{-r}(q_{\mu}\Pi_3(X)|_{S_3(d d \mu)}+q_d\Pi_3(X)|_{S_3(d d d)})\\ &=0\\ t=1,\\ \Pi_1(X)|_{S_1(\mu)} &= e^{-r}(q_{\mu}\Pi_2(X)|_{S_2(\mu \mu)}+q_d\Pi_2(X)|_{S_2(\mu d)})\\ &=2.4459\\ \Pi_1(X)|_{S_1(d)} &= e^{-r}(q_{\mu}\Pi_2(X)|_{S_2(d \mu)}+q_d\Pi_2(X)|_{S_2(d d)})\\ &=0\\ t=0,\\ \Pi_0(X) &= e^{-r}(q_{\mu}\Pi_1(X)|_{S_1(\mu)}+q_d\Pi_1(X)|_{S_1(d)})\\ &=1.33 \end{aligned}\]例 $3$: 年度连续型复利 $r=4\%$,考虑伯努利模型,一只股票 $S_0=40$,每一个序列(三个月)内,要么上涨或下跌 $10\%$,一直进行三个序列;计算美式看跌期权的定价(到期日为 $9$ 个月,行权价格为 $45$)
美式期权和欧式期权计算方法类似,只是过程中可以提前行权,即需要比较提前行权是否比贴现回报更大。
1、 伯努利树

2、 风险中立概率(每个序列-$3$ 个月,均相同)
\[\mu = 1.1,d=0.9,r=0.04/4=1\] \[\left\{ \begin{aligned} &q_\mu + q_d = 1\\ &q_\mu*\mu + q_d*d = e^r\\ \end{aligned} \right. => \left\{ \begin{aligned} &q_\mu = 0.5503\\ &q_d = 0.4497\\ \end{aligned} \right.\]3、 $t=3$ 时,$\Phi(X)=(45-S_3)^+$
4、 定价为:
\[\begin{aligned} t=3,\\ &\Pi_3(X)|_{S_3(\mu \mu \mu)}=0\\ &\Pi_3(X)|_{S_3(\mu \mu d)}=1.44\\ &\Pi_3(X)|_{S_3(\mu d d)}=9.36\\ &\Pi_3(X)|_{S_3(d d d)}=15.84\\ t=2,\\ \Pi_2&(X)|_{S_2(\mu \mu )} \\ &= max\{(45-48.4)^+, e^{-r}(q_{\mu}\Pi_3(X)|_{S_3(\mu \mu \mu)}+q_d\Pi_3(X)|_{S_3(\mu \mu d)})\}\\ &=0.6411\\ \Pi_2&(X)|_{S_2(\mu d )} \\ &= max\{(45-39.6)^+, e^{-r}(q_{\mu}\Pi_3(X)|_{S_3(\mu d \mu)}+q_d\Pi_3(X)|_{S_3(\mu d d)})\}\\ &=5.4,进行提前行权\\ \Pi_2&(X)|_{S_2(d d )} \\ &= max\{(45-32.4)^+, e^{-r}(q_{\mu}\Pi_3(X)|_{S_3(d d \mu)}+q_d\Pi_3(X)|_{S_3(d d d)})\}\\ &=12.6,进行提前行权\\ t=1,\\ \Pi_1&(X)|_{S_1(\mu)} \\ &= max\{(45-44)^+, e^{-r}(q_{\mu}\Pi_2(X)|_{S_2(\mu \mu)}+q_d\Pi_2(X)|_{S_2(\mu d)})\}\\ &=2.7535\\ \Pi_1&(X)|_{S_1(d)} \\ &= max\{(45-36)^+, e^{-r}(q_{\mu}\Pi_2(X)|_{S_2(d \mu)}+q_d\Pi_2(X)|_{S_2(d d)})\}\\ &=9,进行提前行权\\ t=0,\\ \Pi_0&(X) \\ &= max\{(45-40)^+, e^{-r}(q_{\mu}\Pi_1(X)|_{S_1(\mu)}+q_d\Pi_1(X)|_{S_1(d)})\}\\ &=5.5072 \end{aligned}\]B-S 模型
B-S 模型——布朗运动
一个随机过程 $W=(W_t)_{t \ge 0}$,称作布朗运动,当且仅当以下条件完全满足:
- $P(W_0=0)=1$
- 对于所有 $0 \le s < t$,$W_t - W_s \backsim N(0,t-s)$
- 对于任意 $r < s \le t < \mu$,$W_{\mu} - W_t$ 和 $W_s - W_r$ 互相独立
- 所有的路径是连续的
通俗的理解,以 $t$ 作为 $x$ 轴,取值作为 $y$ 轴, 从 $0$ 点出发,
- 对于每个时刻 $t$,$W_t$ 服从 $N(0,t)$ 的正态分布,即大概率取小于 $t$ 的值;小概率取到大于 $t$ 的值;
- 对于整个 $[0,T]$,呈现不规则的折线波动图,类似股票
例 $4$: $\mu < r$,证明 $E(W_{\mu}W_r) = \mu$
\[\begin{aligned} E(W_{\mu}W_r) &= E(W_{\mu}(W_r - W_{\mu} + W_{\mu} ))\\ &=E((W_{\mu}-W_0)(W_r - W_{\mu})) + E(W_{\mu}^2)\\ &=Cov(W_{\mu}-W_0,W_r - W_{\mu}) + E(W_{\mu}-W_0)E(W_r - W_{\mu}) \\ & + Var(W_{\mu}) + [E(W_{\mu})]^2\\ &=0 + 0*0 + \mu + 0^2\\ &=\mu \end{aligned}\]例 $5$: 判断 $X_t = \alpha W_{\frac{t}{\alpha^2}}$,是否为布朗运动?
1、 $X_0 = \alpha W_0 = 0$,符合 2、 对于所有 $0 \le s < t$,
\[\begin{aligned} X_t - X_s &= \alpha (W_{\frac{t}{\alpha^2}} - W_{\frac{s}{\alpha^2}}),符合正态分布\\ E(X_t-X_s) &= \alpha E[W_{\frac{t}{\alpha^2}} - W_{\frac{s}{\alpha^2}}]\\ &=\alpha E[W_{\frac{t}{\alpha^2}}] - \alpha E[W_{\frac{s}{\alpha^2}}]\\ &=0\\ Var(X_t-X_s) &= \alpha^2 (Var(W_{\frac{t}{\alpha^2}})-Var(W_{\frac{s}{\alpha^2}}))\\ &=\alpha^2(\frac{t}{\alpha^2} - \frac{s}{\alpha^2})\\ &=t-s\\ 因此,X_t - X_s \backsim N(0,t-s)\\ \end{aligned}\]3、 对于任意 $r < s \le t < \mu$
\[\begin{aligned} E[(X_{\mu} &- X_t)(X_{s} - X_r)] \\ &= \alpha^4E[(W_{\frac{\mu}{\alpha^2}} - W_{\frac{t}{\alpha^2}})(W_{\frac{s}{\alpha^2}} - W_{\frac{r}{\alpha^2}})]\\ &=0\\ 因此,&X_{\mu} - X_t 和 X_{s} - X_r相互独立 \end{aligned}\]4、 基本的运算,不改变连续性,因此所有路径仍然是连续的
综上,这是布朗运动。
B-S 模型——伊藤引理 Ito’s lemma,解随机微分方程 SDE
伊藤等距 Ito isometry
- 对于布朗运动 $W_t$ 和 $(g_s)_{s \in [0,T]}$,
- 推论 1: 对于布朗运动 $W_t$ 和 $(X_s){s \in [0,T]}$,$(Y_s){s \in [0,T]}$
- 推论 2: 若 $Y_t=1$,则对任意 $0\le a \le b \le T$
- 伊藤积分的性质: 对于布朗运动 $W_t$ 和 $(g_s)_{s \in [0,T]}$,
伊藤过程
- 是一个随机过程 $X_t$ 符合以下随机微分方程等式:
伊藤公式
- 已知伊藤过程 $X_t$,和另一个过程 $Y_t=f(t,X_t)$,则以下等式成立:
- 特殊的,对于布朗运动,即 $X_t=W_t$,$Y_t=f(X_t)=f(W_t)$,
例 $6$: 考虑随机微分方程 $dX_t = \sigma dW_t + \theta(\mu -X_t)dt, t>0, X_0=\mu$;
(a) 证明 $X_t = \mu + \sigma \int_{0}^{t}e^{-\theta(t-s)}dW_s$,(提示: 考虑 $Y_t=(X_t-\mu)e^{\theta t}$)
(b) 求 $E(X_t)$ 和 $Var(X_t)$
- $ 记 f(t, X_t) = Y_t=(X_t-\mu)e^{\theta t}$
- $\frac{\partial f}{\partial t} = \theta (X_t-\mu)e^{\theta t}$,$\frac{\partial f}{\partial x} = e^{\theta t}$,$\frac{\partial^2 f}{\partial x^2} = 0$
- 运用伊藤公式,
- 重新代入 $X_t$
- 两边同时,从 $0$ 到 $t$ 积分
- 即
- 因此
- 数学期望(运用 伊藤积分的性质)
- 方差(运用 伊藤积分的性质 + 伊藤等距)
例 $7$ (几何布朗运动/指数布朗运动): 考虑随机微分方程 $dS_t = \mu S_tdt + \sigma S_tdW_t, S_0=S_0>0$;
(a) 证明 $S_t = S_0e^{(\mu - \frac{1}{2}\sigma^2)t + \sigma W_t}$
(b) 求 $E(S_t)$ 和 $Var(S_t)$
- $ 记 f(t, S_t) = Y_t=ln^{S_t}$
- $\frac{\partial f}{\partial t} = 0$,$\frac{\partial f}{\partial s} = \frac{1}{s}$,$\frac{\partial^2 f}{\partial s^2} = -\frac{1}{s^2}$
- 运用伊藤公式,
- 两边同时,从 $0$ 到 $t$ 积分
- 即
- 因此
- 数学期望
- 方差
B-S 模型——费曼-卡茨公式,解偏微分方程 PDE
- 考虑偏微分方程:
- 可以将其转换成随机变量过程,以及可通过伊藤公式求解 SDE 得到 $\Phi(X_T)$
- 则,原方程的的解,$f(t,x)$ 为
- 证明思路: 记 $Y_t = e^{-rt}f(t,x)$,再运用伊藤公式求解 $Y_t$,最终方程两边同时求数学期望即可得到等式。
例 $8$ (B-S偏微分方程求解):已知如下偏微分方程,出于简化,仅求解 $f(0,x) 即可 $
\[\begin{aligned} \frac{\partial f}{\partial t}(t,x) + &rx\frac{\partial f}{\partial t}(t,x) + \frac{1}{2}\sigma^2x^2\frac{\partial^2 f}{\partial x^2}(t,x) - rf(t,x)=0\\ &f(T,S_T) = max\{S_T - K, 0\} = (S_T - K)^+ \end{aligned}\]- 跟费曼·卡茨公式对齐,$\mu(t,x)=rx$,$\sigma(t,x)=\sigma x$
- 对应的伊藤过程 $dX_s = rX_s + \sigma X_sdW_s$,实际上,这是个指数布朗运动,由例 $7$ 可知 $X_T = X_0e^{(r - \frac{1}{2}\sigma^2)T + \sigma W_T}$,即 $S_T = S_0e^{(r - \frac{1}{2}\sigma^2)T + \sigma W_T}$
- 则,原方程的的解,$f(0,S_t)$ 为
- 记 $d_+=\frac{ln^{\frac{S_0}{K}}+(r+\frac{\sigma^2}{2})T}{\sigma \sqrt{T}}$,
- $d_{-}=\frac{ln^{\frac{S_0}{K}}+(r-\frac{\sigma^2}{2})T}{\sigma \sqrt{T}}$,
- $N(0,1)$ 为标准正态分布
- $N(d)$ 为标准正态分布的累积分布函数
- 该解即为 B-S 模型下,看涨期权在 $t=0$ 的定价
B-S 模型——几何布朗运动+期权定价
市场假设 $S$
- 即为例 $7$ 中的指数布朗运动,即股票的价格满足随机微分方程
- 并且对应的解,$S_t = S_0e^{(\mu - \frac{1}{2}\sigma^2)t + \sigma W_t}$
B-S PDE 偏微分方程
- $f(t, St)$为对应$△S$的标的物的衍生品的价格,则其投资价值满足$dI(t) = df(t, St) - △dSt$
- 对$f(t, St)$运用伊藤公式,化简可得
- 代入化简可得
- 若 $△ = \frac{\partial f}{\partial s}$,且$dI(t)=rI(t)dt$时,则可以得到风险中立的$f(t,S_t)$所满足的等式
- 即 风险中立的$f(t,S_t)$所满足的等式/偏微分方程:
常见的期权定价
- 求解偏微分方程,即可得到期权定价,例 $8$ 即为看涨期权定价的求解过程。
- 记,
- $d_+=\frac{ln^{\frac{S_0}{K}}+(r+\frac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}}$,
- $d_{-}=\frac{ln^{\frac{S_0}{K}}+(r-\frac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}}=d_+ - \sigma \sqrt{T-t}$,
- $N(0,1)$ 为标准正态分布
- $N(d)$ 为标准正态分布的累积分布函数
- 看涨期权在$t$时刻的定价为:
- 看跌期权在$t$时刻的定价为:
小 结
| 模型 | 伯努利模型 | B-S模型 |
|---|---|---|
| 市场假设 | 伯努利树 | 指数布朗运动 |
| 定价计算 | 从后往前,用风险中立概率和数学期望进行贴现 | 求解偏微分方程 -> 求解随机微分方程 -> 求解复杂运动过程的数学期望 |