网络科学 学了啥(上) —— 网络指标+比特币的商业分析
微信公众号内容地址: https://mp.weixin.qq.com/s/0V3QX8TeHffPWrxPyEBpOQ
该课程的全名为:数据驱动的商业和行为分析(Data-driven Business and Behavior Analysis,简称 DBBA)。前半部分,主要学习基于网络科学的方法论进行宏观商业分析;而后半部分,则主要学习基于代理模型的方法论进行微观行为分析。
简单来说,网络科学就是将一些场景(如金融交易、社交关系)抽象成网络/图结构,并通过研究复杂网络的性质,提升对宏观系统的洞见。参考教材为 A First Course in Network Science,参考工具包为 Python 的 Networkx。(在 Networkx 官网教程中,也会对网络指标的计算过程、网络生成的算法进行详细介绍,因而本文在概念部分只进行简单介绍,重点探索在实践中的应用。)
课程上主要分为两大部分 —— 网络的指标、网络的生成和模拟。并且,课程以一个比特币交易网络的商业分析任务为作业,来加深理解。
作为上篇,本文主要介绍网络的指标,以及这些指标在比特币网络的商业分析中的应用。
网络的指标
基础指标
常见的网络的核心基础指标如下:
- $G$ 表示一个网络,$N$ 表示网络的总节点数,$L$ 表示网络的总边数。
- 网络的分类
-
无向、无权重
:如 Facebook 的用户关系网络。
-
无向、有权重
:如交通网络,边的权重表示两地的距离。
-
有向、无权重
:如维基百科页面链接网络,边的方向表示单向链接。
-
有向、有权重
:如邮件,边的方向表示邮件发送方向,边的权重表示总共发送的邮件数。
-
无向、无权重
- $L_{max}$ 表示 $N$ 个节点的网络,理论上,边的数量的最大值。
- 对于无向网络来说,$L_{max} = \frac{N(N-1)}{2}$
- 对于有向网络来说,$L_{max} = N(N-1)$
- $d$ 表示网络的密度,$d = \frac{L}{L_{max}}$,社交网络一般密度都很低。
-
$k_i$ 表示网络中 i 节点的度,即该节点拥有的边的个数,也可以理解为该节点的邻居个数。
- 对于有向网络来说,$k_{i}^{in}$ 表示入度,指向该节点的边的个数;$k_{i}^{out}$ 表示出度,该节点向外的边的个数;$k_{i}^{tot}$ 表示总度,入度和出度之和,即不考虑边的方向时,该节点拥有的边的个数。
- $< k >$ 表示整个网络中,所有节点的度的平均值,即每个节点平均的邻居数。
- 对于有权重网络来说,$s_i$ 表示强度,即该节点所有边的权重之和;同样的定义,也有 $< s >$ 表示网络的平均强度,有向网络中有 $s_i^{in}$、$s_i^{out}$、$s_i^{tot}$。
以下是一些常见网络的基础指标数值:
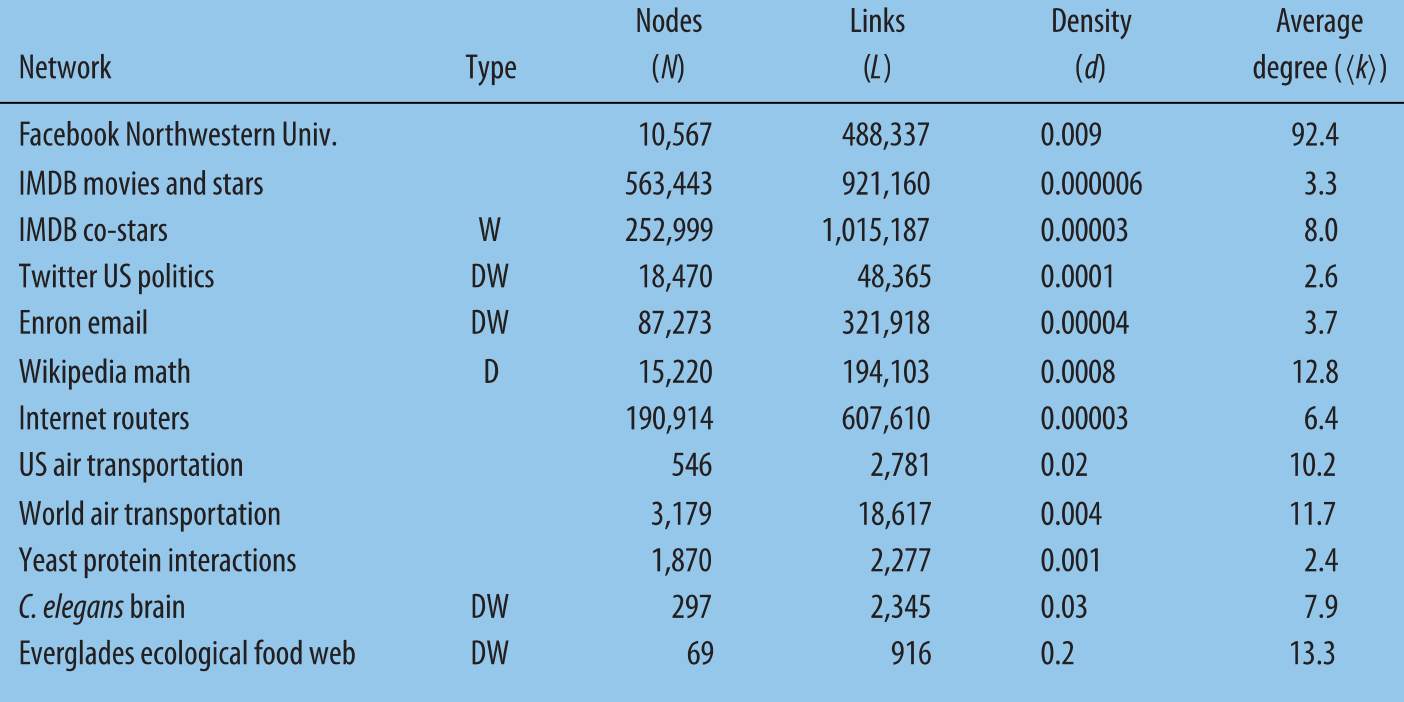
举例来说,在下图的有向权重网络示例中,
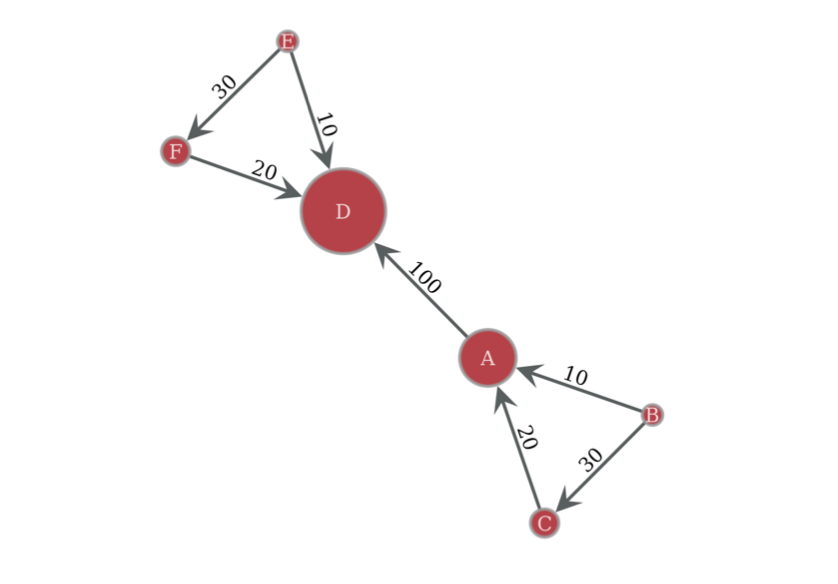
- $N = 6$,$L = 7$
- $L_{max}=N(N−1)=30$,$d = \frac{L}{L_{max}} = \frac{7}{30}$
- 对节点 A 来说,$k_A^{in}=2$,$k_A^{out}=1$,$k_A^{tot}=3$
- 对节点 A 来说,$s_A^{in} = 30$,$s_A^{out} = 100$,$s_A^{tot} = 130$
- $< k^{tot} > = \frac{2+2+3+3+2+2}{6} = \frac{7}{3}$,$< s^{tot} > = \frac{50+40+130+130+40+50}{6} = \frac{220}{3}$
同样的,也可以使用代码进行计算,
## 有向图生成
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
G = nx.DiGraph()
G.add_nodes_from(['A', 'B', 'C', 'D', 'E', 'F'])
G.add_weighted_edges_from([('B', 'C', 30), ('B', 'A', 10), ('C', 'A', 20), ('A', 'D', 100), ('E', 'F', 30), ('E', 'D', 10), ('F', 'D', 20)])
# 绘制图形
pos = nx.spring_layout(G) # 布局算法
nx.draw(G, pos, with_labels=True)
# 绘制带权重的边
nx.draw_networkx_edge_labels(G, pos, edge_labels=nx.get_edge_attributes(G, 'weight'))
plt.show()
# 节点数
N = G.number_of_nodes()
# 边数
L = G.number_of_edges()
# 理论上的最大节点数
L_max = N*(N-1)
# 密度
d = round(nx.density(G), 2)
# A节点的度和强度
k_A_in = G.in_degree('A')
k_A_out = G.out_degree('A')
k_A_tot = G.degree('A')
s_A_in = G.in_degree('A', weight='weight')
s_A_out = G.out_degree('A', weight='weight')
s_A_tot = G.degree('A', weight='weight')
# 平均度和强度
avg_k_in = round(sum(dict(G.in_degree()).values()) / N, 2)
avg_k_out = round(sum(dict(G.out_degree()).values()) / N, 2)
avg_k_tot = round(sum(dict(G.degree()).values()) / N, 2)
avg_s_in = round(sum(dict(G.in_degree(weight='weight')).values()) / N, 2)
avg_s_out = round(sum(dict(G.out_degree(weight='weight')).values()) / N, 2)
avg_s_tot = round(sum(dict(G.degree(weight='weight')).values()) / N, 2)
print(f'{N=}, {L=}, {L_max=}, {d=}')
print(f'{k_A_in=}, {k_A_out=}, {k_A_tot=}, {s_A_in=}, {s_A_out=}, {s_A_tot=}')
print(f'{avg_k_in=}, {avg_k_out=}, {avg_k_tot=}')
print(f'{avg_s_in=}, {avg_s_out=}, {avg_s_tot=}')
N=6, L=7, L_max=30, d=0.23
k_A_in=2, k_A_out=1, k_A_tot=3, s_A_in=30, s_A_out=10 0, s_A_tot=130
avg_k_in=1.17, avg_k_out=1.17, avg_k_tot=2.33
avg_s_in=36.67, avg_s_out=36.67, avg_s_tot=73.33
同质性指标
同质性指标,目的是分析网络中的节点有多“相似”,或者理解为相似的节点间有连接的概率。比较常用的如下:
- Connectivity,表示网络的连通性。
- 对于无向网络来说,连通表示任意两个节点之间至少存在一条路径可连接。
- 对于有向网络来说,弱连通表示不考虑边的方向前提下,任意两个节点之间至少存在一条路径;强连通则表示即使考虑边的方向,任意两个节点之间至少存在一条路径。
- 按照是否连通对网络进行拆解,每个部分叫 Component,拥有最多节点的部分为最大连通子网络。
- $l_{AB}$ 表示最短路径,即 A 节点和 B 节点之间最短路径的长度。
- $< l >$,表示整个网络中,所有的两个节点之间最短路径的平均值。只有(强)连通网络才有该指标,且该指标计算较为耗时,$O(N^2)$。
- 如果 $ < l > \approx log(N)$,表示该网络的平均路径较短。特别的,联系社交网络的六度分隔理论(世界上相互不认识的两人,通过较少的中间人就能建立起联系),即该网络下 $ < l > \approx 6$。
- $l_{max}$ 表示直径,即整个网络中,所有最短路径长度之中的最大值。只有(强)连通网络才有该指标,且该指标计算较为耗时,$O(N^2)$。
-
Clustering Coefficient
,聚类系数,表示该节点的两个邻居之间有连接的概率,也可以理解为该节点周围现在的“三角形”数量和潜在的所有“三角形”数量的比例。
-
平均聚类系数
,整个网络平均来看,一个节点的两个邻居之间有连接的概率。
- $< l >$,表示整个网络中,所有的两个节点之间最短路径的平均值。只有(强)连通网络才有该指标,且该指标计算较为耗时,$O(N^2)$。
仍然以上图的网络为例,
- 若不考虑边的方向,这是连通网络;若考虑边的方向,这是弱连通网络(比如,D->A 无路径)
- $l_{CD} = 120$
- 若不考虑边的方向,考虑边的权重,在该连通网络中,$< l > = \frac{10+20+100+…+10+20+30}{6*5/2} = 80$,$l_{max} = l_{CF} = 140$
- 若不考虑边的方向,不考虑边的权重,对于节点 A 来说,聚类系数为 $\frac{1}{3*2/2} = 0.33$
同样的,也可以使用代码进行计算,
# 最短路径
l_CD = nx.shortest_path_length(G, 'C', 'D', weight='weight')
# 不考虑边的方向,考虑权重,计算平均最短路径和直径
avg_l = nx.average_shortest_path_length(G.to_undirected(), weight='weight')
l_max = nx.diameter(G.to_undirected(), weight='weight')
# 不考虑边的方向,不考虑权重,计算聚类系数
clustering_coefficient = nx.clustering(G.to_undirected())
avg_clustering_coefficient = round(sum(clustering_coefficient.values()) / N, 2)
print(f'connected = {nx.is_connected(G.to_undirected())}, weakly_connected = {nx.is_weakly_connected(G)}, strongly_connected = {nx.is_strongly_connected(G)}')
print(f'{l_CD=}')
print(f'{avg_l=}, {l_max=}')
print(clustering_coefficient)
print(f'{avg_clustering_coefficient=}')
connected = True, weakly_connected = True, strongly_connected = False
l_CD=120
avg_l=80.0, l_max=140
{'A': 0.3333333333333333, 'B': 1.0, 'C': 1.0, 'D': 0.3333333333333333, 'E': 1.0, 'F': 1.0}
avg_clustering_coefficient=0.78
异质性指标
与同质性指标相反,异质性指标目的是分析网络中的节点“差异”有多大,尤其是关注中心节点 Hubs,因而主要是中心节点识别算法。比较常用的如下:
-
Degree Centrality
,根据节点的度或强度的大小进行排序。
- 异质性衡量,$\kappa = \frac{< k^2 >}{< k > ^2}$,若该值明显比 1 大,则系统异质性明显。
-
Closeness Centrality
, 计算某节点到其他节点的平均最短路径长度的倒数,即衡量该节点与其他节点间的距离。
-
Betweenness Centrality
,计算网络的所有最短路径里经过该节点的比例,即衡量该节点在网络中的桥梁作用。
值得注意的是,Closeness 和 Betweenness 两个指标,与最短路径相似,这带来了两点特殊:
- 最短路径的计算较为耗时,因而这两个指标,单节点计算时间复杂度为 $O(N^2)$,整个网络遍历完为 $O(N^3)$。
- 默认边的权重越大,路径越长。因此如果边的权重越大表示越重要,则指标计算时,需要取权重的倒数(使得权重越大,对应的路径越短,越容易成为“最短路径”)
仍然以上图的网络为例,
- A 和 D 节点的度均为 3,强度均为 130
- 若不考虑边的方向,考虑边的权重,A 节点的 Closeness Centrality 值为 $\frac{1}{(10+20+100+110+120)/5} = 0.014$
- 若不考虑边的方向,考虑边的权重,A 节点的 Betweenness Centrality 值为 $ \frac{\frac{1}{2}+1+1+1+1+1+1}{10} = 0.65$,具体过程如下表格所示:
| 最短路径 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | - | AB | AC | AD | ADE | ADF |
| B | - | BC / BAC | BAD | BADE | BADF | |
| C | - | CAD | CADE | CADF | ||
| D | - | DE | DF | |||
| E | - | EF / EDF | ||||
| F | - |
代码计算如下:
def top(dist, num=5):
return [(id,score) for id, score in sorted(dist, key = lambda p: -p[1])][:num]
# 不考虑边的方向,考虑权重
# 度排名
print(top(list(nx.degree(G, weight='weight'))))
# 使用度,计算异质性
degrees = list(dict(nx.degree(G, weight='weight')).values())
print(f'kappa = {np.mean(np.power(degrees, 2)) / np.power(np.mean(degrees), 2)}')
# closeness 排名;默认weight越大,最短路径越长 -> weight需要注意,如果weight越大,表示越重要/接近,需要取倒数
print(top(list(nx.closeness_centrality(G.to_undirected(), distance='weight').items())))
# betweenness 排名;默认weight越大,最短路径越长 -> weight需要注意,如果weight越大,表示越重要/接近,需要取倒数
print(top(list(nx.betweenness_centrality(G.to_undirected(), weight='weight').items())))
[('A', 130), ('D', 130), ('C', 50), ('F', 50), ('B', 40)]
kappa = 1.3016528925619835
[('A', 0.013888888888888888), ('D', 0.013888888888888888), ('B', 0.0125), ('E', 0.0125), ('C', 0.011363636363636364)]
[('A', 0.65), ('D', 0.65), ('B', 0.0), ('C', 0.0), ('E', 0.0)]
社区探索
网络的社区探索,跟机器学习等模型中的多分类算法有相似之处,即通过社区划分,使得社区之间特征尽量差异化,社区之内特征尽量一致化,以便进行更多的探索。该领域范围较广,算法多且复杂,因而在此不做过多介绍,读者可以自行阅读探索。
比特币网络的商业分析
数据源
金融相关的数据,在常用的网站上(如 Yahoo Finance、Bloomberg)均可以查到,然后通过 Networkx 把数据按需转换成对应的网络结构。也可以去公开的网络科学数据库进行下载网络文件,如 https://snap.stanford.edu/data/index.html。
本次的比特币网络数据源自,https://networks.skewed.de/net/bitcoin
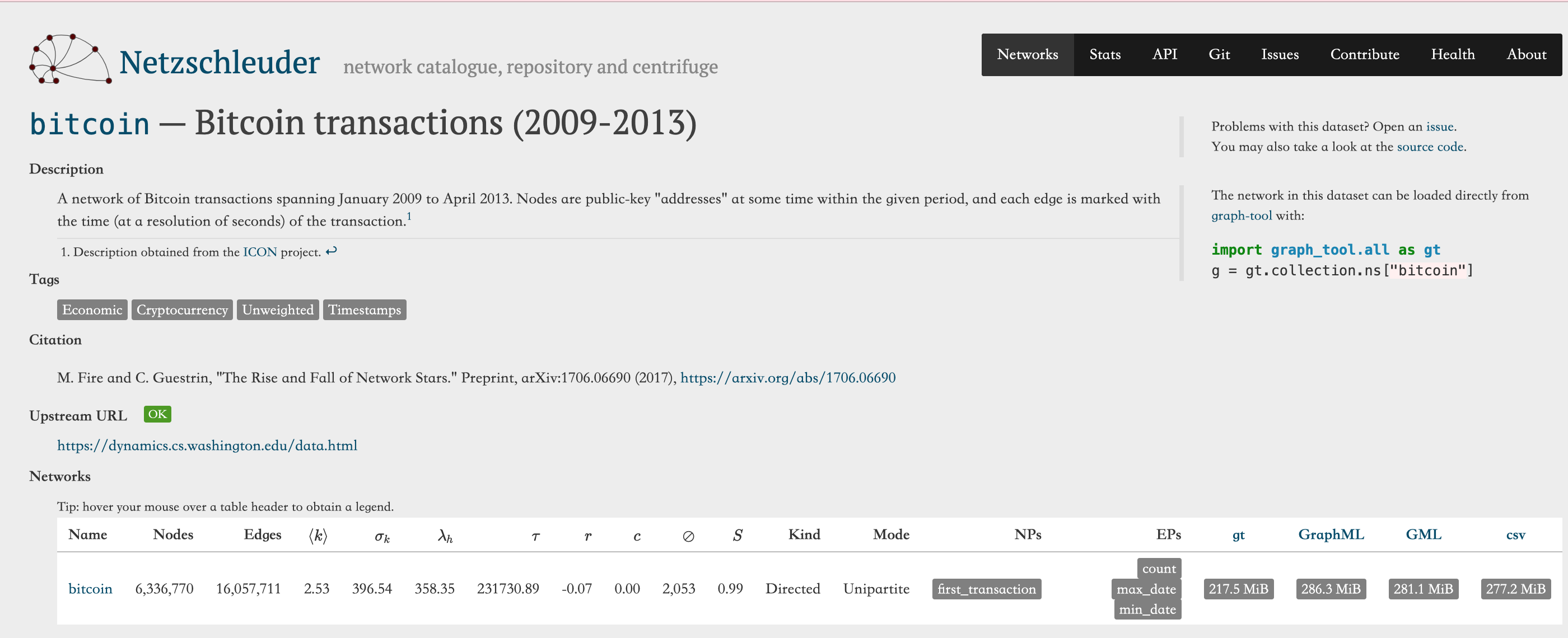
经过 graph_tool 工具包按照 first_transaction 属性进行处理后,可以得到 2013.09 - 2013.12 期间的 .graphml 网络文件(包含一次比特币泡沫,用于分析探索)。
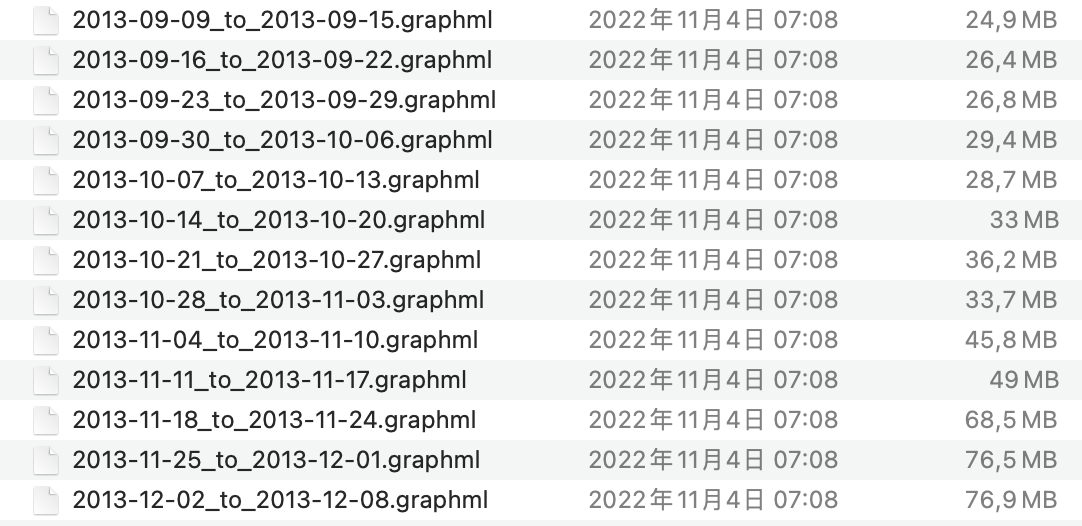
数据理解
除了 Networkx,本次也使用了 igraph 工具包,两者之间的 Graph 也提供了很方便的转换接口。
通过 igraph 加载网络文件,过滤得到最大连通子网络,同时进行 summary 操作,输出结果如下:
*** process 2013-09-09_to_2013-09-15.graphml
IGRAPH D--- 105516 229005 --
+ attr: id (v), no_transactions (e), qty (e)
IGRAPH D--- 59574 148959 --
+ attr: id (v), no_transactions (e), qty (e)
...
...
*** process 2013-12-02_to_2013-12-08.graphml
IGRAPH D--- 314132 709238 --
+ attr: id (v), no_transactions (e), qty (e)
IGRAPH D--- 165772 463363 --
+ attr: id (v), no_transactions (e), qty (e)
finish, GSCCs length = 13
简单小结下,该数据集包含了 13 个比特币交易网络。每个网络为一周的数据和,有向有权重;节点表示用户,属性为 id,数量在 5w-16w 个;边表示交易,属性为 qty 和 no_transactions,数量在 14w-46w 条。该数据量,按照百万次每秒的计算能力来看,对于 $O(N^2)$ 的指标来说,会是小时级别的任务。
基础指标和同质性指标
通过 pandas 整合计算结果,并进行展示:
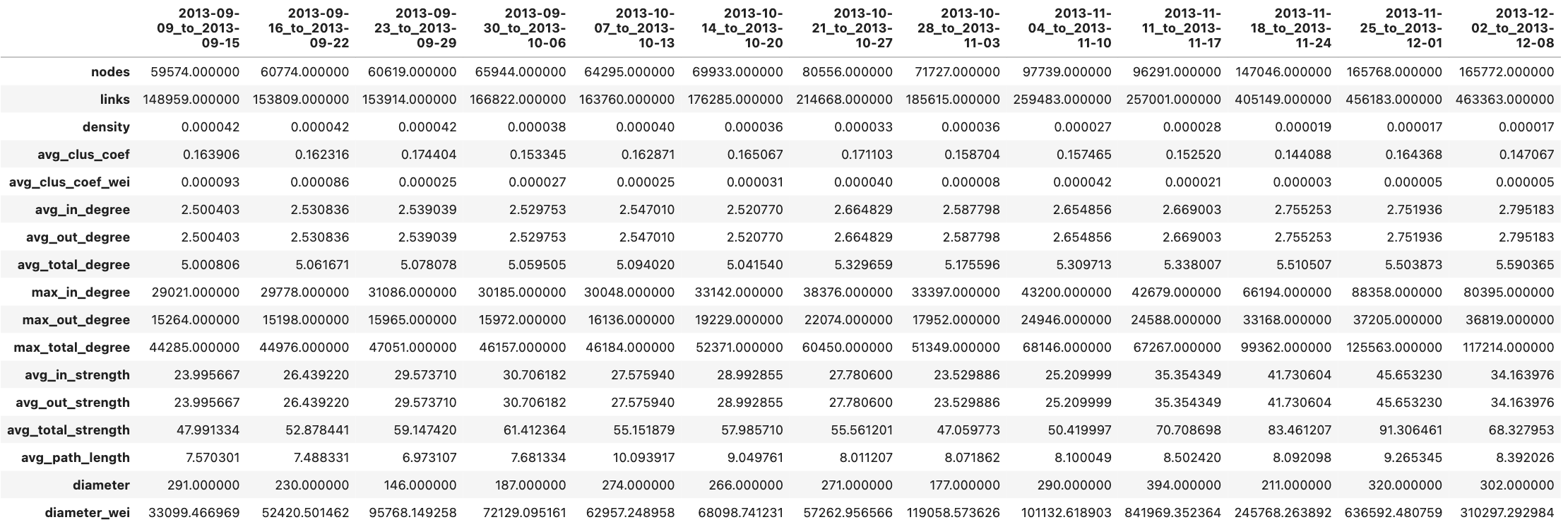
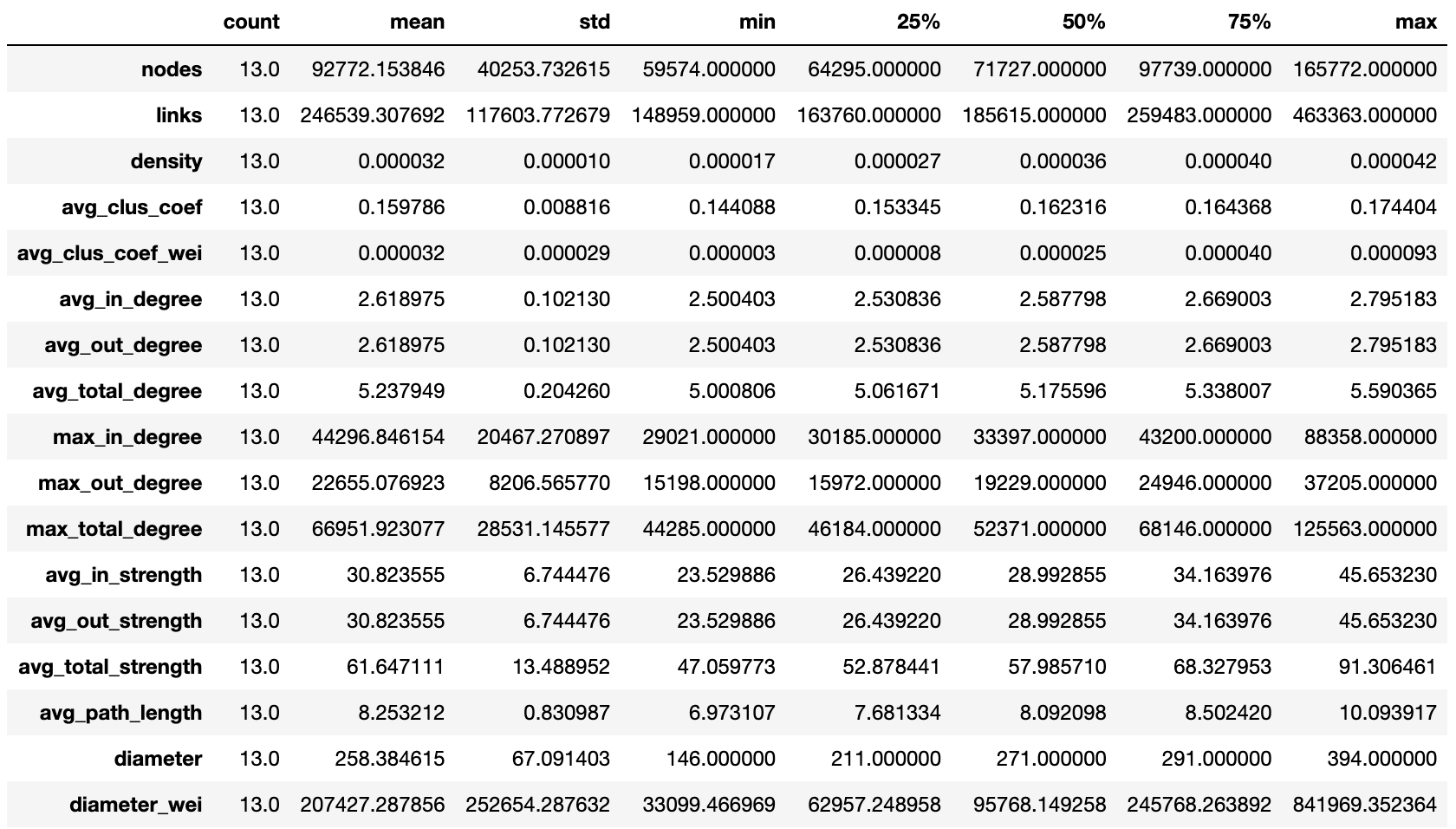
先进行总体上的分析:
-
边
的数量基本是节点数量的 3 倍,这也合理的解释了密度值很低的原因(根据密度的计算公式,L ~ O(N^2),即密度值正常的话,边数量应该和节点数量的平方量级相当)。因而可以总结,该交易网络是稀疏网络。
- 不考虑权重时,网络的聚类系数在 0.15 左右,相对较高。
-
平均的度
约为 5,即平均每个账户每周进行 5 笔交易;而最大的度则接近 6w,与平均水平差距很大,暗示该网络存在较大的异质性,需要对中心节点进行研究和关注。
-
度
和强度之间的数量差异,反应了权重的均值,大约在 10-15。
- 从平均最短路径长度来看,略大于 6,一定程度上符合六度分隔理论。即互相不认识的用户,经过 6-7 次的交易,就可以实现流通。
接下来以时间为轴,观察指标随着时间的变化情况。
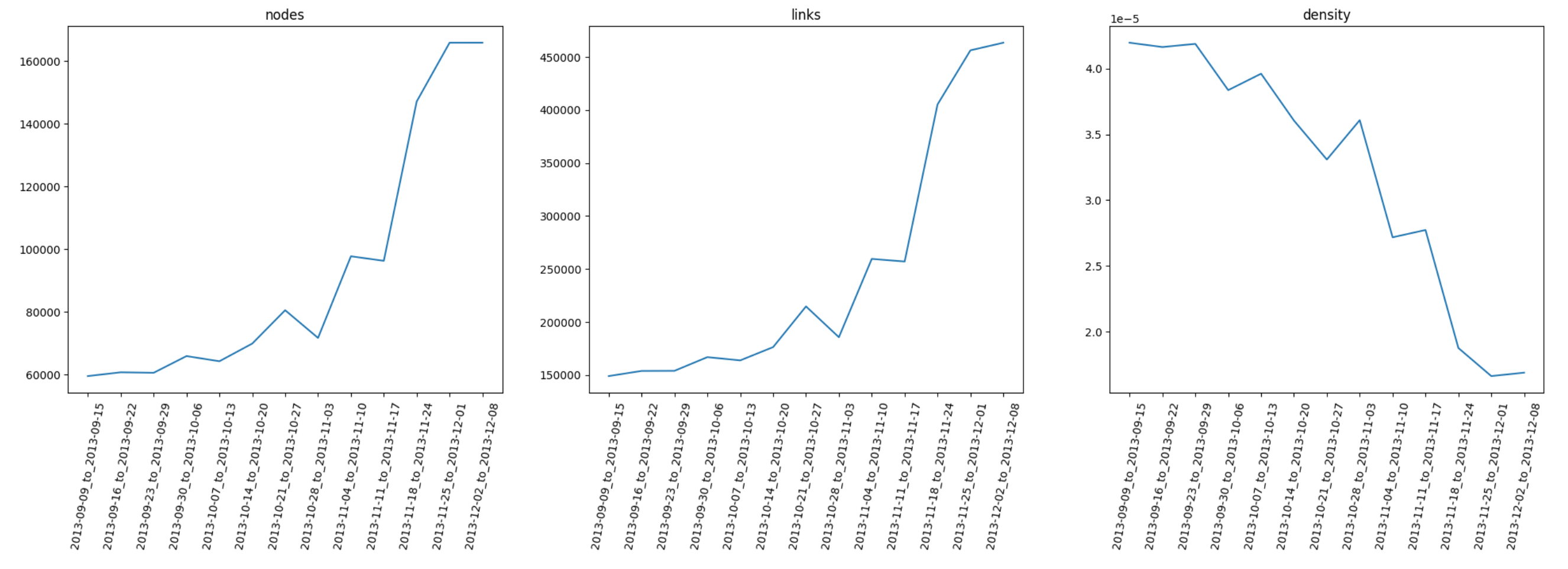
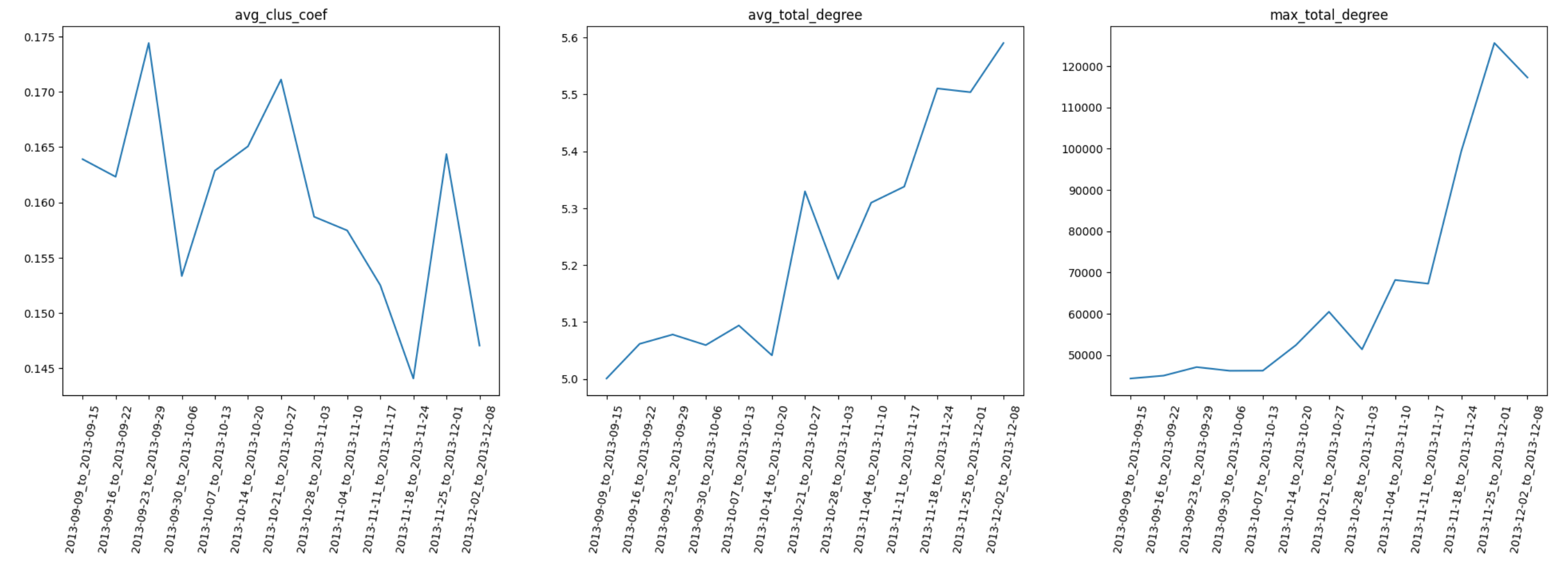
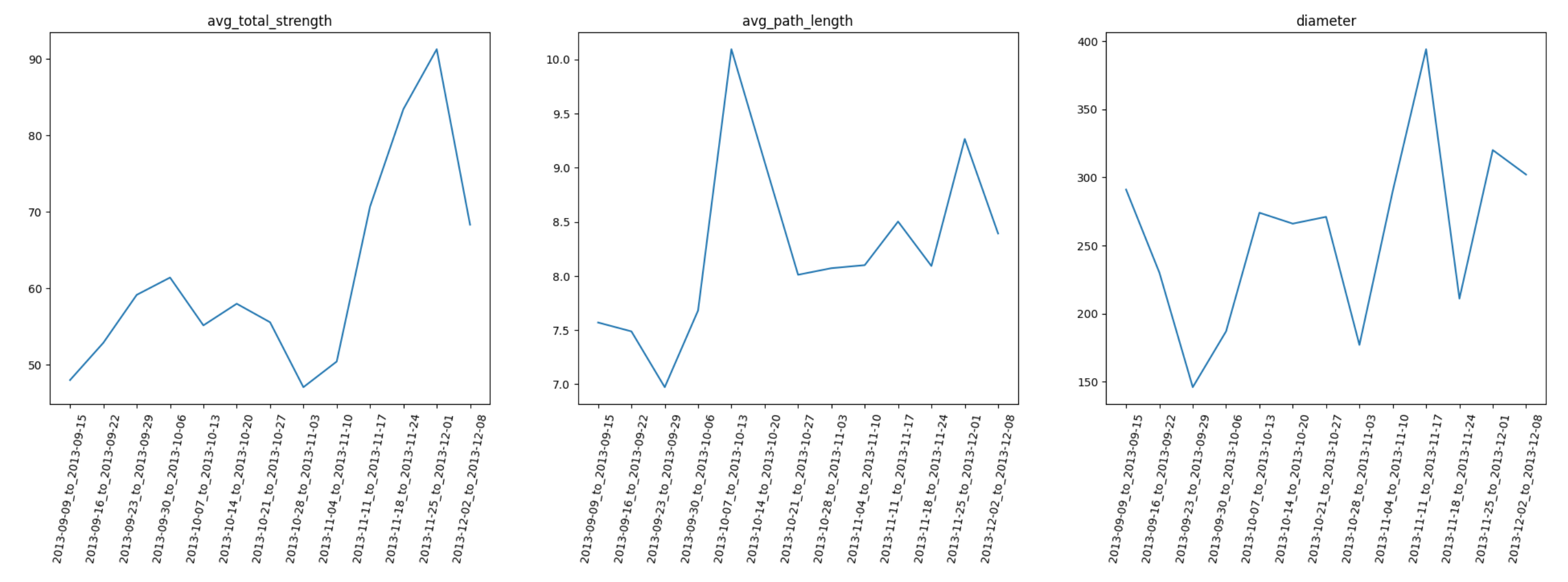
同样的,先对数据进行总结和初步分析:
-
节点
数和边数都在不断增加,并且在 12 月前明显加快,随后几乎进入停滞;同时,边和节点的增长速度保持线性相关性,因此密度反而会不断减小($d \approx \frac{L}{N^2}$)。
-
聚类系数
整体上呈现下降趋势,于 11 月下旬到达低点,后迅速回升,12 月初又迅速下跌。
-
平均度
、最大度、平均强度均保持增长,但是之间的增长速度并不匹配。以 12 月初为例,平均度在增长,但是最大度和平均强度却在下跌。
-
平均最短路径长度
和直径,总体上在保持增长,12 月前上涨后,12 月初出现了下跌。
上述分析中,会发现 12 月初是一个值得关注的时间点,在这附近,节点数、边数、聚类系数、平均最短路径长度和直径均为先增后减;12 月初时,平均度在增长,但是最大度和平均强度却在下跌。实际上,这个时间点对应的就是当时比特币的泡沫,因而结合这些指标,我们可以尝试进行一些解释:
- 泡沫前:节点数、边数增加,大量新用户进入系统进行交易;聚类系数增加,但总体上仍然在偏低值,说明交易数增加改善了系统的交易结构,但系统中的“三角形”数量仍然处在较低值;此时结合平均最短路径长度和直径也保持上升,说明系统更接近于环形而非网形结构,系统容错能力下降,即系统中部分边的消失,就会影响很多节点之间的交易,网络中繁荣与泡沫并存。
- 泡沫后:节点数、边数几乎停止增加,很少有新用户看好系统进入交易;聚类系数进一步下降,系统网型结构进一步被破坏;而最短路径等数据也保持下降,则在一定程度上有利于止损,剩余的参与交易的活跃用户慢慢的恢复系统的交易结构。结合最大度和平均强度的下降,说明中心节点在慢慢减少交易,有可能是通过抛售后慢慢退出系统。
以上是利用这些指标尝试分析的一次探索作业,从项目维度上来看,实际上还缺少验证集测试、显著性校验等严谨的证明环节。
异质性指标,Hubs
这里我们分别在 9 月、10 月、11 月选择一周的网络,使用 Betweenness Centrality 计算得出排名前十的中心节点:
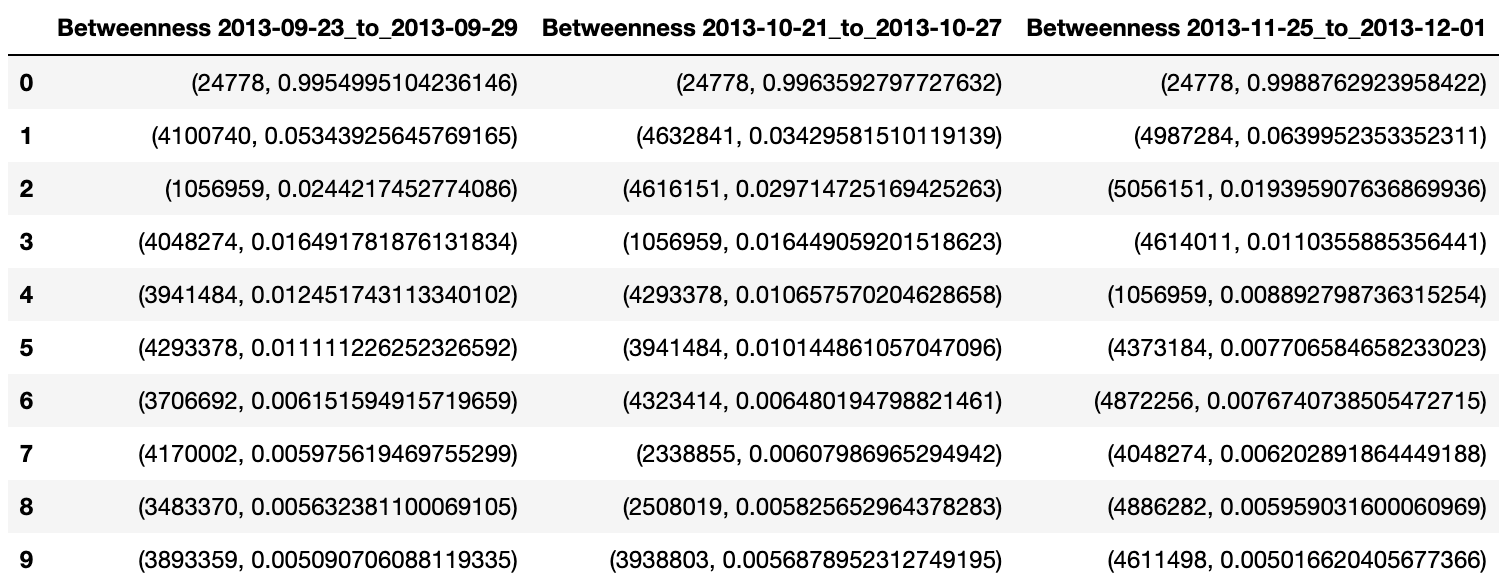
可以看出,三个时间段,均有 24778 这个中心节点,且中心度的值极端的高。其他中心节点则不断交替,甚至有的可能在后来退出了系统。
要进一步的分析中心节点对系统的影响,还需要结合网络生成、网络模拟等方法论。例如,在网络攻击模拟中,当去掉节点 24778 后,系统的最大连通网络的规模将会迅速缩减到原来的 50% 不到,充分体现了经济学中的“大而不能倒”(too big to fail)。
总 结
基于网络指标进行数据分析的一大好处,便是过程可见和具有可解释性。
除此之外,它也不仅限于本身就是类网络结构的场景,通过对节点和边的特殊设计,即特征化,也可以应用于更多抽象的任务中。例如,有类似的论文在探索,以公司为节点、两家公司拥有共同的投资人为边、共同的投资人数量为边的权重,来对初创企业的成功率进行建模分析。(举例来说,在该“网络”下,可以用数据验证以下猜想:越是中心的节点,从投资人和其他公司处得到的指导也可能越多,其获得生存甚至高速发展的概率也越高。)
总的来说,基于网络指标的数据分析,仍然偏宏观的静态分析,即充分理解和解释现有数据。但实际上商业分析中仍有很多“如果”的场景,这便需要后续介绍的宏观和微观的动态分析方法来继续探索了:
- 如果把小场景中的结论拓展到更一般的环境下(网络生成)
- 如果宏观环境发生变化(网络模拟)
- 如果微观个体发生变化(代理模型 Agent-based Model,简称 ABM)
- …